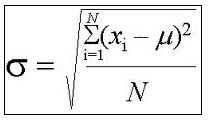Critical Chi-Square Values Calculator

Some more information about critical values for the Chi-Square distribution probability so you can better understand the outcome that this calculator provides and how it relates to hypothesis testing.

The Chi-Square statistics is one of the most broadly used test statistics, most notably for testing for the independence of two variables, as well as for the test of goodness of fit.

What are Chi-Square Critical Values

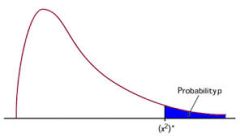
In general terms, critical values are points at the tail(s) of a certain distribution so that the area under the curve for those points to the tails is equal to the given value of \(\alpha\).

These points are usually used as threshold points of what would be considered to be a point "far enough" in the tail of the distribution. And then, based upon this definition, Critical Chi-Square Values are specific critical points for a given Chi-Square distribution.

How do you find the critical value for chi-square?

For a two-tailed case, the critical values correspond to two points on the left and right tails of the distribution, with the property that the sum of the area under the curve for the left tail (from the left critical point) and the area under the curve for the right tail is equal to the given significance level \(\alpha\).

For a left-tailed case, the critical value corresponds to the point on the left tail of the distribution, with the property that the area under the curve for the left tail (from the critical point to the left) is equal to the given significance level \(\alpha\).

For a right-tailed case, the critical value corresponds to the point on the right tail of the distribution, with the property that the area under the curve for the right tail (from the critical point to the right) is equal to the given significance level \(\alpha\)

What is the critical value of a 0.05 in chi-square test?

This is a good example to show how the Chi-Square distribution works. First of all, this requested critical value cannot be computed without specifying the Chi-Square of interest, for which you need to indicate the corresponding number of degrees of freedom.

For this example, let's assume the number of degrees of freedom is df = 10. In that case, by either looking at a Chi-Square distribution table, or using this calculator, we find that the required critical value is \(\chi_c^2 = 18.307\).

What does a chi-square test tell you?

It depends on the specific test. The Chi-Square statistics is used to test for one population variance, for goodness of fit and for independence, among others, and its specific interpretation must be made in the context of each specific test.

But there elements that hold true among all possible uses of a Chi-Square test. For example, when then Chi-Square test statistic exceeds the Chi-Square critical value(s), then the null hypothesis of the test will be rejected.

Critical Points for Different Distributions

Critical points are threshold points in the tail(s) of the distribution, and it applies all the same to any distribution. Of then times you will use a distribution table to get those critical values, or sometimes you will use a calculator, depending on what you have available

For other critical value calculators, please check our z-critical value calculator , which is used for the normal distribution. or our t-value critical value calculator , which is used for the t-distribution, which means that you also need to indicate the corresponding degrees of freedom.

Also, for the F-distribution (that needs to get two degrees of freedom specified), you can use this F-critical value calculator.

The advantage of using our critical value calculators is that aside from getting the critical values needed along with any relevant calculation, you will get a neat graph depicting the graphical situation of the critical values found.