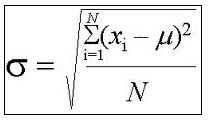Descriptive Statistics Calculator of Grouped Data
Instructions : This descriptive statistics calculator for grouped data calculates the sample mean, variance and standard deviation for grouped data. Grouped data is specified in class groups instead of individual values. It comes with ranges of values associated with a frequency. For example, one range could be 2 - 6 and the frequency could be, say, 8, another range could be 7 - 10, with a frequency of 4, etc.
How to Use this Descriptive Statistics Calculator for Grouped Data?
Calculating descriptive statistics for grouped data is similar to computing descriptive statistics for a regular sample of data, only that in the case of grouped data, we have less information about the data. We don't know the precise values of the data, but we have ranges where the data lies in
This calculator will compute the mean, standard deviation, variance, median and quartiles, using estimates of the mean point of the interval information provided.
In principle, in order to compute descriptive statistics for grouped data we need to estimate a proxy for the values that belong to a certain class/interval, by computing the midpoint of the interval. Such midpoint will serve as the best possible representative of all the points in the class.
Once the midpoints are computed, the sample mean, variance and standard deviation are obtained as follows:
\[ \bar X = \frac{ 1}{n}\left(\sum_{i=1}^n M_i \cdot f_i \right) \] \[ var(X) = \frac{ 1}{n-1}\left(\sum_{i=1}^n M_i^2 \cdot f_i - \frac{1}{n}\left(\sum_{i=1}^n M_i \cdot f_i \right)^2 \right) \] \[ SD(X) = \sqrt{\frac{ 1}{n-1}\left(\sum_{i=1}^n M_i^2 \cdot f_i - \frac{1}{n}\left(\sum_{i=1}^n M_i \cdot f_i \right)^2 \right)}\]If instead you are dealing with ungrouped data, you can use our descriptive statistics calculator for ungrouped data .
Also, you may be interested in learning more about graphical representations of the sample data, using tools like the histogram and the box-plot .