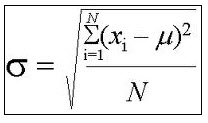Power Calculator Minimum Sample Size – Testing for One Mean
Instructions: This statistical power calculator computes, showing all the steps, the minimum required sample size (\(n\)) to reach a given target statistical power (\(1-\beta\)), when testing for a one population mean. You need to provide the significance level (\(\alpha\)), the target power, the effect size (\(d\)) and the type of tail (left-tailed, right-tailed or two-tailed). If you don't know the exact value of the effect size, choose between small, medium or large effect size in the form below:
More About this Power Calculator
This statistical power calculator allows you to compute the minimum required sample size \(n\) to reach a target statistical power, when you know the significance level (\(\alpha\)), the sample size, the effect size (\(d\)) and the type of tail (left-tailed, right-tailed or two-tailed). This is usually referred as an A-Priori Power calculation . Check here for a Post-Hoc Power Calculator
What exactly is statistical power?
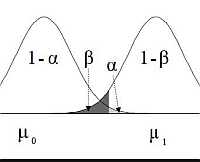
The statistical power of a test corresponds to the probability of rejecting a null hypothesis. This is, it is the probability of detecting a true effect. Technically, the statistical power is 1 minus the probability of a type 2 error, or \(1 - \beta\).
Power and Effect Size
Typically, the most difficult information to get is the effect size, defined as Cohen's d. If you don't have the actual value of \(d\), you can approximate it by categorizing it into one of three categories: small, medium and large effect size .
One way of estimating a magnitude of the effect size, if not available directly, is to use meta-analysis. This technique consists in analyzing many studies on similar phenomena, and get an "average" of the effect size obtained in those studies. This is the way of getting some kind of ecological average effect size . This process will lead likely to a very rough estimate, which often times is better than nothing.