Decimal to Fraction Calculator
Instructions: Use this calculator to convert a given decimal that you provide to fraction, showing all the steps. Please type in one decimal number (for example, a number like '3.4673' or a number like '.345279') in the form below:
About this Decimal to Fraction Calculator
What is a decimal? A decimal refers to a way of expressing numbers using the number of ten as its base, as well as powers of ten and tenth parts.
In simple words, decimals are numbers as you know them, this, you have a sequence of digits (numbers between 0 and 9), followed possibly by tenth parts, represented by a dot "." and a sequence of digits
Example of digit: For example, 45.34556 and 0.5678 are digits. Digits that have only a "0" on the left of the "." are usually written like .4534, for the sake of brevity.
How do you convert a decimal to a fraction?
The strategy is simple: we need to try to "eliminate" the decimals (the digits on the right of the ".") by multiplying the number by a power of 10.
Once you do that, you take note of the power of 10 you used to achieve that, because then you will use that to convert the given number to a decimal.
For example, if you had the number 2.34, you need to multiply by 100 to "eliminate" the decimals, so you get \(2.34 \cdot 100 = 234\). In this case, the number after "eliminating" the decimals is N = 234 and the power of 10 used is \(10^2 = 100\).
Decimal to Fraction Formula
Step 1: Let D a number with decimal digits. You multiply D by a power of 10, so that there are no more digits to the right of the ".", or as some would say, so there are no decimals in the number.
Step 2: From the previous step, you have the power of 10 you used to "eliminate" the decimals, say that number is \(10^k\), and say that N is the result after "eliminating decimals".
Step 3: The formula for expressing the given number to a fraction is
\[ D = \displaystyle\frac{N}{10^k}\]and possibly, you may want to reduce the fraction on the right to its lowest expression.
Decimal to Fraction Chart
There are classic charts that provide you a clear snapshot of the equivalence of the most commonly used fractions and their decimal conversions.
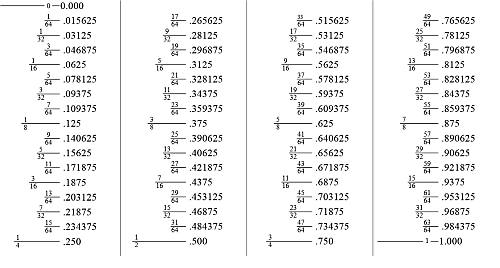
Advantages and disadvantages of using a chart versus the formula for decimals to fraction
- Using a chart is direct: You just look at the chart and get the decimal - fraction conversion immediately
- The problem with the chart is that the precise decimal or fraction you are looking for is not there
- Using the conversion formula, you are assured that you can convert ANY number, but you actually need to work on the calculation.
Calculators about fractions and percentages
Naturally, as you probably realize now, fractions, decimals and percentages are tightly related. And often times, they are just different formats to represent the same information in a more convenient way for a given context.
For example, using a percent to fraction calculator does a similar job as this decimal to fraction calculator, with the difference that you will need to convert the decimal to percent first.
Naturally, you may be facing the reverse situation. Maybe you want to convert a fraction to a decimal, which is simply the common algorithm of division Arithmetics. Notice that converting a fraction to a decimal can lead to a finite decimal number, or potentially to a repeating decimal.
For example, the fraction \(\displaystyle \frac{3}{5}\) corresponds simply to 0.6 (a simple, finite decimal), but the fraction \(\displaystyle \frac{1}{3}\) corresponds to the repeating decimal 0.33333.....

Example: Conversion of Decimal to Fraction
Question: Calculate the number 3.4563 as a fraction.
Solution:
You have provided the following decimal \(D = \displaystyle 3.4563\), and the objective is to convert it to a fraction.
Step 1: We need to multiply \(D = 3.4563\) by a power of 10, so that the resulting expression does not have decimal values, to the right of the '.' sign.
Step 2: This is simply done by counting the number of digits to the right of the period '.'. For the number provided, we have \(k = 4\) digits to the right of the period.
Therefore, the power of 10 needed is \(10^{k} = 10^{4} = 10000\). Hence, we find that
Step 3: Hence, we find that
\[ N = D \times 10^k = 3.4563 \times 10^{4} \] \[ = 3.4563 \times 10000= 34563 \]So then, by dividing both sides by \(10000\), we get
\[ 3.4563 = \displaystyle \frac{34563}{10000} \]and since the fraction found is already simplified, it is concluded that the simplest fraction equivalent of \(3.4563\) is \(3.4563\).
Therefore, the expression of the decimal as a fraction in its simplest terms is \(\displaystyle 3.4563 = \frac{ 34563}{ 10000}\), which concludes the calculation.
Example 2
Question Express .625 as a fraction.
Solution:You have provided the following decimal \(D = \displaystyle 0.625\), and the objective is to convert it to a fraction.
Step 1: We need to multiply \(D = 0.625\) by a power of 10, so that the resulting expression does not have decimal values, to the right of the '.' sign.
Step 2: This is simply done by counting the number of digits to the right of the period '.'. For the number provided, we have \(k = 3\) digits to the right of the period.
Therefore, the power of 10 needed is \(10^{k} = 10^{3} = 1000\). Hence, we find that
Step 3: Hence, we find that
\[ N = D \times 10^k = 0.625 \times 10^{3} \] \[ = 0.625 \times 1000= 625 \]So then, by dividing both sides by \(1000\), we get
\[ 0.625 = \displaystyle \frac{625}{1000} \]Further simplifying the fraction that resulted from the previous step, we found that: \[\frac{ 625}{ 1000} = \frac{ 125 \times 5}{ 125 \times 8} = \frac{ \cancel{ 125} \times 5}{ \cancel{ 125} \times 8} = \frac{ 5}{ 8}\]
Therefore, the expression of the decimal as a fraction in its simplest terms is \(\displaystyle 0.625 = \frac{ 5}{ 8}\), which concludes the calculation.
Example 3
Question Compute .8 as a fraction
Solution:
You have provided the following decimal \(D = \displaystyle 0.8\), and the objective is to convert it to a fraction.
Step 1: We need to multiply \(D = 0.8\) by a power of 10, so that the resulting expression does not have decimal values, to the right of the '.' sign.
Step 2: This is simply done by counting the number of digits to the right of the period '.'. For the number provided, we have \(k = 1\) digits to the right of the period.
Therefore, the power of 10 needed is \(10^{k} = 10^{1} = 10\). Hence, we find that
Step 3: Hence, we find that
\[ N = D \times 10^k = 0.8 \times 10^{1} \] \[ = 0.8 \times 10= 8 \]So then, by dividing both sides by \(10\), we get
\[ 0.8 = \displaystyle \frac{8}{10} \]Further simplifying the fraction that resulted from the previous step, we found that: \[\frac{ 8}{ 10} = \frac{ 2 \times 4}{ 2 \times 5} = \frac{ \cancel{ 2} \times 4}{ \cancel{ 2} \times 5} = \frac{ 4}{ 5}\]
Therefore, the expression of the decimal as a fraction in its simplest terms is \(\displaystyle 0.8 = \frac{ 4}{ 5}\), which concludes the calculation.