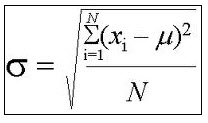Uniform Probability Calculator
Instructions: Compute uniform distribution probabilities using the solver below. Please type the lower limit \(a\), the upper limit \(b\), and define the event for which you want to compute the probability for:
More about the uniform distribution probability
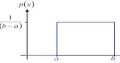
Here is a little bit of information about the uniform distribution probability so you can better use the the probability calculator presented above: The uniform distribution is a type of continuous probability distribution that can take random values on the the interval \([a, b]\), and it zero outside of this interval. The main properties of the uniform distribution are:
- It is continuous (and hence, the probability of any singleton event is zero)
- It is determined by two parameters: the lower (a) and upper (b) limits
- The population mean is \(\frac{a+b}{2}\), and the population standard deviation is \(\sqrt{\frac{(b-a)^2}{12}}\).
Using the above uniform distribution curve calculator , you will be able to compute probabilities of the form \(\Pr(a \le X \le b)\), with its respective uniform distribution graphs .
Type the lower and upper parameters a and b to graph the uniform distribution based on what your need to compute. If you need to compute \(\Pr(3 \le X \le 4)\), you will type "3" and "4" in the corresponding boxes of the script for the two-tailed test, for example.
Other common continuous probability distribution calculators that you can also use are the normal probability calculator , exponential probability calculator and the t-distribution calculator .