Simplifier for Fractions

Instructions: Use this simplifier for fractions to reduce a fraction you provide in the form box below.

About this simplifier for fractions calculator

This calculator allows you to simplify a fraction that is provided by reducing the fraction to its lowest possible expressions. You need to give the calculator a fraction, by just simply typing it.

For example, you can write something simple like '3/9', or something like '(1+3)/(6+8)'. Then, when you have written a valid fraction expression, you just need to click on the button that says "Calculate". Then, you will be presented with step-by-step calculation of the fraction simplification.

If you provide a fraction with operations in the numerator and/or denominator, this calculator will first conduct those calculations.

How to simplify a fraction

The reduction of a fraction to minimum terms is quite simple, and it involves simplifying any common factor that the numerator and denominator may have.

What are the steps for fraction simplifier?

Step 1: Identify clearly the numerator and denominator of the fraction
Step 2: Find the factors for each numerator and denominator
Step 3: Cancel out those common factors

Why would want to reduce fractions?

There are many reasons for considering fraction reduction. For one, a reduced fraction has the same value as the original, but it is simpler, it makes sense to keep a simplified version of the original fraction.

It depends on the case obviously. Perhaps the original fraction has a specific meaning, and it is not useful to reduce it. So you need to evaluate, depending on the circumstances, whether a simplification is in order or not.

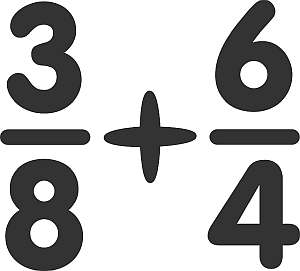
$Simplification of a fraction$

Example: Calculating the simplification of a fraction

Simplify the following fraction $\displaystyle \frac{32}{48}$.

Solution:

We need to simplify the following given fraction: $\displaystyle \frac{32}{48}$.

The following calculation is obtained:

$ \displaystyle \frac{32}{48}$

We can factor out 16 for both the numerator and denominator.

$ = \,\,$

$\displaystyle \frac{ 16 \times 2}{ 16 \times 3}$

Now we cancel 16 out from the numerator and denominator.

$ = \,\,$

$\displaystyle \frac{ \cancel{ 16} \times 2}{ \cancel{ 16} \times 3}$

After canceling 16 out, we get this simplified fraction.

$ = \,\,$

$\displaystyle \frac{ 2}{ 3}$

which concludes the calculation.

Example: Another fraction reduction

Simplify now the following fraction \(\displaystyle \frac{3+9}{6\times 3}.

Solution:

We need to simplify the following given fraction: $\displaystyle \frac{3+9}{6\cdot 3}$.

The following calculation is obtained:

$ \displaystyle \frac{3+9}{6\cdot 3}$

Simplifying the integers that can be multiplied: $\displaystyle 6\times3 = 18$

$ = \,\,$

$\displaystyle \frac{3+9}{18}$

Reducing the integers that can be added together: $\displaystyle 3+9 = 12$

$ = \,\,$

$\displaystyle \frac{12}{18}$

We can factor out 6 for both the numerator and denominator.

$ = \,\,$

$\displaystyle \frac{ 6 \times 2}{ 6 \times 3}$

Now we cancel 6 out from the numerator and denominator.

$ = \,\,$

$\displaystyle \frac{ \cancel{ 6} \times 2}{ \cancel{ 6} \times 3}$

After canceling 6 out, we get this simplified fraction.

$ = \,\,$

$\displaystyle \frac{ 2}{ 3}$

which concludes the calculation.

Other fraction calculators

Fractions are ubiquitous objects in Algebra, and are used in so many contexts. Fraction calculators play an important role at aiding you with seeing how the process is completed, and how the algebra is carried out.

The key process of a fraction reduction is the calculation of the greatest common divisor, which is the largest value by which we can simplify both numerator and denominator.

Also, in a different facet of fractions, especially in the more elementary levels, you maybe interested in dealing with mixed fractions, and how to convert them to regular fractions.

Fractions will appear everywhere, as a part of general algebraic expression, and within the context of polynomial calculations, and functions in general.