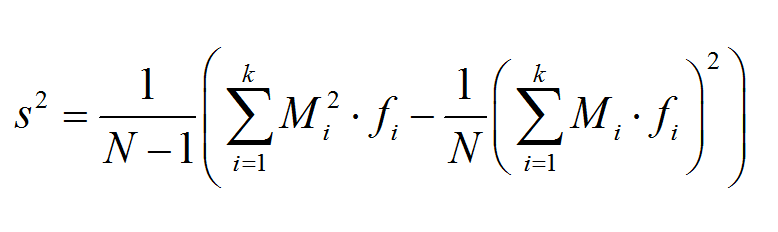One Way ANOVA Calculator
Instructions: This calculator conducts One-Way ANOVA for a group of samples, with the purpose of comparing the population means of several groups. Please type the sample data for the groups you want to compare and the significance level \(\alpha\), and the results of the ANOVA test for independent samples will be displayed for you (Compare up to 6 groups. Please leave empty the columns that you will not use):
One Way Analysis of Variance Calculator
More about the One-Way ANOVA test so you can better understand the results delivered by this solver. First of all, ANOVA or Analysis of Variances is one of the most important fields in Statistic. The reason for this is that is goes into the core of analyzing the variation exhibited samples, by breaking down the total variation into various different sources of variation.
The most basic use of ANOVA is to test for the difference between the populations for several groups (2 or more). Let us recall that a t-test is used to compare the means of two groups, so then ANOVA is some sort extension that allows to perform comparisons for two or more groups.
As with any other hypothesis test, ANOVA uses a null and the alternative hypothesis. The null hypothesis is a statement that claims that all population means are equal, and the alternative hypothesis is the hypothesis that not all means are equal (observe that this does NOT imply that all means are unequal, it implies that al least one pair of means is unequal).
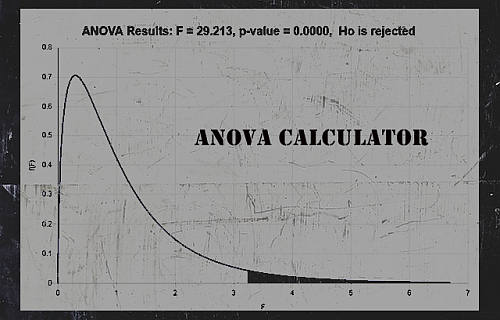
How do you calculate an ANOVA?
Running an ANOVA test is a little bit like running any other parametric test, and you will need then some assumptions to be met. The main assumptions required to perform a one-way ANOVA are:
- The dependent variable (DV) needs to be measured at least at the interval level
- The groups must come from normally distributed populations
- The groups must come from normally populations with equal population variances
If the results of the ANOVA are significant, this is, the null hypothesis is rejected, we can perform a Post-Hoc test to assess exactly which pairs differ significantly. Examples of Post-Hoc tests are Fisher's LSD, Tukey's test, Bonferroni correction, etc.
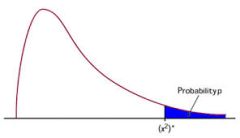
The null hypothesis of an ANOVA test are rejected when the F-statistics exceeds the value of the critical F-ratio that is calculated, based on the corresponding degrees of freedom.
When you have k groups and a total sample size of N, then the numerator degrees of freedom are dfN = k - 1, and the denominator degrees of freedom are dfD = N - k - 2.
When some of the assumption are not met (specifically the second are third), there are corrective options for some more robust statistics. When there are serious violations to the assumptions, it would be more appropriate to use a non-parametric alternative, like Kruskal-Wallis' Test.
This ANOVA calculator with steps provides you with enough information to reject or to fail to reject the null hypothesis, based on the F-ratio that is computed. If the null hypothesis is computed, you will need to conduct a Post-Hoc test.
Why a t-test is not used instead
Two independent sample T-tests are designed to conduct a comparisons between two groups. When you have more than two groups, the only way to compare is to conduct several pairwise comparisons.
Each of those pairwise comparisons has a certain probability of a type I error, so the family-wise type I error is the probability that at least one of those comparisons leads to a type I error. When many comparisons are done, then the family-wise probability of a type I error gets greatly inflated
A one-way ANOVA is designed to compare two or more sample means, but if you want to compare two sample means, then it may be more efficient to use directly our t-test for two independent samples .
Non-Parametric Alternatives to ANOVA
ANOVA requires certain assumptions to hold, namely, normality and homogeneity of variances. It is known that ANOVA is relatively robust to violation of assumptions, especially if they are mild. But what to do when the assumptions are simply not met?
In that case you can use our Kruskal-Wallis test calculator, which is the non-parametric equivalent to ANOVA. One advantage of the Kruskal-Wallis test is that you can use it even with ordinal data, for which using ANOVA would not be a good idea.