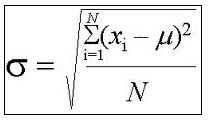More About this Interquartile Calculator

The Interquartile Range is a very commonly used measure of dispersion, to assess how spread the data of a distribution are. The same role is fulfilled by the standard deviation , but the interquartile range has a specific characteristic that makes usable for ordinal data, and it is also less sensitive to outliers.

The interquartile range is used also in the box-plot associated to sample data, which often times is used to assess distributional properties of data, same as with a histogram.

One advantage of the interquartile range as a dispersion measurement is that it is more resistant to the presence of outliers, unlike the standard deviation.

How to Compute the Interquartile Range?

The Interquartile Range is defined as the difference between the first quartile (\(Q_1\)) and third quartile (\(Q_3\)). Mathematically, this is written as:

\[ IQR = Q_3 - Q_1 \]

How to compute the Interquartile in Excel

The easiest way to compute the interquartile range using Excel is by using the formula: "=QUARTILE(data, 3) - QUARTILE(data, 1)", by simply typing it in Excel.

One thing to keep in mind is that there are different conventions to compute quartiles for sample data. Indeed, if you have a sample and try to compute the quartiles with Excel, you will get a different answer than what you get say with Minitab.

The reason for this discrepancy is the why the different statistical software deal with interpolation.

Interpretation of the interquartile range

As we already mentioned, the interquartile range (IQR) is a measure of dispersion of a distribution. Graphically, it corresponds to the size of the box in a box-plot , which is a graphical device to visualize a distribution and detect outliers .

If instead of computing the interquartile range you need to compute a generic percentile, you can try our percentile calculator , which will show the percentile calculation with all the steps.

Not only visually but outliers can also be detected and found using a formula. The "1.5 times IQR" rule can be also be used as the basis for an outliers calculator, where any point that 1.5 x IQR beyond the first and third quartiles is considered an outlier.